BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Hukum-hukum rangkaian dan metoda-metoda yang digunakan di dalam menganalisis rangkaian penahan tersebut, seperti : hukum Ohm, hukum Kirchhoff, analisis Simpul, analisis Mesh/Loop, teorema Thevenin, teorema Norton, dan lain-lain, akan terbukti dapat juga digunakan untuk menganalisis rangkaian yang mengandung induktor dan kapasitor.
Sejalan perkembangan teknologi,maka perkembangan dibidang teknologi elektronika pun berkembang dengan pesat. Hal ini ditandai dengan munculnya berbagai macam produk peralatan elektronika. Dengan semakin majunya bidang elekronika, maka wajib bagi mahasiswa/i elektro umumnya
dan elektronika khususnya untuk mengetahui segala beluk-beluk elektronika, seperti komponen,menghitung tegangan,arus,hambatan,daya. Arus bolak-balik (AC/alternating current) adalah arus listrik dimana besar dan arahnya arus berubah-ubah terhadap waktu.
BAB II
PEMBAHASAN
A.TEGANGAN, ARUS DAN DAYA
1.Pengertian Arus Bolak Balik
Definisi Arus bolak-balik. Arus listrik atau AC (Alternating Current), atau arus bolak balik adalah arus listrik yang arahnya selalu berubah secara periodic terhadap waktu. Biasanya dihasilkan oleh generator atau dynamo. Nilai arus dan tegangan bolak-balik selalu berubah-ubah menurut awktu, dan mempunyai pola grafik simetris berupa fungsi sinusoda.
Sementara itu pengertian adaptor atau definisi adaptor adalah alat untuk mengubah tegangan dan jenis arus listrik bolak-balik menjadi searah, dengan besar tegangan disesuaikan menurut keperluan. Misalnya dalam pemakaian alat-alat listrik yang memerlukan arus searah seperti radio, tape recorder, dan lampu senter dapat menggunakan arus bolak balik (AC), asalkan lebih dahulu dilewatkan adaptor. Arus bolak-balik selalu mempunyai nilai puncak gelombang atas dan puncak gelombang bawah. Dalam peristiwa mencapainya nilai puncak gelombang atas dan puncak gelombang bawah maka dikatakan telah mencapai satu (1) gelombang penuh. Nilai puncak gelombang atas dan puncak gelombang bawah sering pula disebut nilai dari puncak ke puncak ( nilai peak to peak ),Pengertian arus bolak-balik telah dijelaskan pada bagian sebelumnya, yaitu arus yang besar dan arahnya berubah-rubah setiap waktu ( setiap saat ). Berdasarkan pengertian tersebut, dapat diartikan bahwa arus bolak-balik berbentuk gelombang.Berdasarkan difinisi tersebut maka bentuk gelombang arus bolak-balik dapat dibedakan menjadi 3 macam bentuk gelombang yaitu :
Sementara itu pengertian adaptor atau definisi adaptor adalah alat untuk mengubah tegangan dan jenis arus listrik bolak-balik menjadi searah, dengan besar tegangan disesuaikan menurut keperluan. Misalnya dalam pemakaian alat-alat listrik yang memerlukan arus searah seperti radio, tape recorder, dan lampu senter dapat menggunakan arus bolak balik (AC), asalkan lebih dahulu dilewatkan adaptor. Arus bolak-balik selalu mempunyai nilai puncak gelombang atas dan puncak gelombang bawah. Dalam peristiwa mencapainya nilai puncak gelombang atas dan puncak gelombang bawah maka dikatakan telah mencapai satu (1) gelombang penuh. Nilai puncak gelombang atas dan puncak gelombang bawah sering pula disebut nilai dari puncak ke puncak ( nilai peak to peak ),Pengertian arus bolak-balik telah dijelaskan pada bagian sebelumnya, yaitu arus yang besar dan arahnya berubah-rubah setiap waktu ( setiap saat ). Berdasarkan pengertian tersebut, dapat diartikan bahwa arus bolak-balik berbentuk gelombang.Berdasarkan difinisi tersebut maka bentuk gelombang arus bolak-balik dapat dibedakan menjadi 3 macam bentuk gelombang yaitu :
1) Gelombang Sinusoidal,
2) Gelombang Kotak ( segi empat ), dan
3) Gelombang segitiga
2.Sumber Arus Bolak Balik
Tegangan bolak-balik sinusoidal, tersedia dari bermacam-macam sumber. Sumber arus bolak-balik pada umumnya dihasilkam oleh pembangkit tenaga listrik seperti Pembangkit Listrik Tenaga Air, Pembangkit Listrik Tenaga Uap, Pembangkit Listrik Tenaga Gas, Pembangkit Listrik Tenaga Angin dan Pembangkit Listrik Tenaga Surya ( Panas matahari ).
Ada pula pembangkit listrik yang sifatnya mudah dibawa ( portable ). Gambar 3, menunjukkan contoh beberapa pembangkit arus bolak-balik.
1.generating plant
2.portable ac generator
3.wind-power station
4. Pembangkit TL
5.Pembangkit T.Angin
3.Cara Kerja Generator
Generator arus bolak- balik adalah alat(dinamo) yang dapat mengubah energi mekanik menjadi energi listrik arus bolak-balik melalui proses induksi elektromagnetik . Generator arus bolak- balik sering disebut juga sebagai alternator atau generator AC (alternating current) atau juga generator singkron. Alat ini sering dimanfaatkan di industri untuk mengerakkan beberapa mesin yang menggunakan arus listrik sebagai sumber penggerak. Generator arus bolak-balik dibagi menjadi dua jenis, yaitu:
a. Generator arus bolak-balik 1 fasa
b. Generator arus bolak-balik 3 fasa
a. Generator arus bolak-balik 1 fasa
b. Generator arus bolak-balik 3 fasa
Komponen generator AC ada stator, rotor, sikat, exciter, AVR, pengatur generator dabearing .
a. Rotor
Rotor adalah bagian dari motor listrik atau generator yang berputar pada sumbu rotor. Perputaran rotor di sebabkan karena adanya medan magnet dan lilitan kawat email pada rotor. Sedangkan torsi dari perputaran rotor di tentukan oleh banyaknya lilitan kawat dan juga diameternya.
b. Stator
Stator adalah kebalikan dari rotor, stator adalah bagian pada motor listrik atau dinamo listrik yang berfungsi sebagai stasioner(yang diam) dari sistem rotor. Dan stator inilah yang mengeluarkan tegangan bolakbalik. Stator terdiri dari badan generator yang terbuat dari baja yang berfungsi melindungi bagian dalam generator, kotak terminal dan name plate pada generator. Inti Stator yang terbuat dari bahan ferromagnetik yang berlapis-lapis dan terdapat alur-alur tempat meletakkan lilitan stator. Lilitan stator yang merupakan tempat untuk menghasilkan tegangan.
c. Sikat
Sikat adalah bagian yang menghubungkan jangkar atau stator dengan kabel tujuannya agar kabel tidak ikut berputar .
d. Exciter
Exciter adalah bagian penguat yang digunakan generator untuk membangkitkan sumber tenaga sebagai penggerak mula generator
e. AVR
AVR adalah singkatan dari Automatic Voltage Regulator yang mengatur tegangan yang berubah-rubah, dan terdiri dari satu kumparan .
Prinsip Kerja Generator, Prinsip dasar generator arus bolak-balik menggunakan hukum Faraday yang menyatakan jika sebatang penghantar berada pada medan magnet yang berubah-ubah, maka pada penghantar tersebut akan terbentuk gaya gerak listrik. proses terjadinya tenaga mekanik tenaga listrik ada beberapa syarat .
1. Adany fluks yang ditimbukan oleh dua buah kutub magnet.
2. Adanya kawat penghantar.
3. Adanya putaran yang menyebabkan penghantar memotong fluks2 magnet.
Rotor yang ada pada generator AC pada dasarnya membutuhkan suatu alat yang berfungsi untuk memutar rotor tersebut misalnya angin, air, uap dan lain-lain. Setelah rotor berputar, dari perputaran rotor itulah yang akan menghasilkan arus listrik.
dalam generator sebenarnya terdiri dari banyak lilitan dalam masing-masing fasa yang terdistribusi pada masing-masing alur stator dan disebut “Lilitan terdistribusi”. Diasumsikan rotor berputar searah jarum jam, maka fluks medan rotor bergerak sesuai lilitan jangkar. Satu putaran rotor dalam satu detik menghasilkan satu siklus per detik atau 1 Hertz (Hz).
4.Arus Dan Tegangan Listrik Bolak-Balik
Sumber arus bolak-balik adalah generator arus bolak-balik yang prinsip kerjanya pada perputaran kumparan dengan kecepatan sudut ω yang berada di dalam medan magnetik. Sumber ggl bolak-balik tersebut akan menghasilkan tegangan sinusoida berfrekuensi f. Apabila generator tersebut dihubungkan dengan suatu penghantar R dan menghasilkan tegangan maksimum sebesar Vmax, maka tegangan dan arus listrik yang melewati penghantar.
Tegangan sinusoida dapat dituliskan dalam bentuk persamaan tegangan sebagai fungsi waktu, yaitu :
Tegangan yang dihasilkan oleh suatu generator listrik berbentuk sinusoida. Dengan demikian, arus yang dihasilkan juga sinusoida yang mengikuti persamaan :
Dengan :
V = Tegangan Listrik AC
I = Arus Listrik AC
Vmax = Tegangan maksimum
Imax = Arus maksimum
ω = Kecepatan sudut (2πf)
DASAR LISTRIK BOLAK-BALIK (AC)
- Asal usal Tegangan dan Arus Listrik Bolak-Balik
Suatu bentuk gelombang tegangan listrik bolak-balik dapat digambarkan seperti pada Gambar 1 di bawah ini.




Gambar 1. Bentuk Gelombang Tegangan Listrik Bolak-Balik.
Pesamaan tegangan sesaat
Dimana
v = Tegangan sesaat
Vm = Tegangan Maksimum
- = Frekuensi = 1/t (Hz)
T = Periode = waktu untuk satu gelombang
ω = kecepatan sudut = 2πƒ = 2π/T = radian perdetik
Frekuensi dalam listrik AC merupakan banyaknya gelombang yang terjadi dalam satu detik. Jika waktu yang diperlukan oleh satu gelombang disebut periode (T) maka.
jika generator mempunyai P kutub dan berputar sebanyak N kali dalam satu menit, maka frekuensi mempunyi persamaan
P = Jumlah kutub generator
N = Jumlah putaran permenit (rpm)
Sudut Fase dan Beda Fase
Dalam rangkaian listrik arus bolak-balik sudut fase dan beda fase akan memberikan informasi tentang tegangan dan arus. Sedangkan beda fase antara tegangan dan arus pada listrik arus bolak-balik memberikan informasi tentang sifat beban dan penyerapan daya atau energi listrik. Dengan mengetahui beda fase antara tegangan dan arus dapat diketaui sifat beban apakah resistif, induktif atau kapasitif.
- Tegangan Efektif dan Arus Efektif
Tegangan listrik arus bolak – balik yang diukur dengan multimeter menunjukan tegangan efektif. Nilai tegangan dan arus efektif pada arus bolak – balik menunjukan gejala yang sama seperti panas yang timbul jika dilewati arus searah :
= 0.707 Tegangan Maksimum
Ief
|
=
|
= 0.707 Imax
|
3.Respon Elemen
- Resistor dalam arus bolak – balik
Rangkaian yang terdiri dari sebuah sumber tegangan bolak – baliik dan sebuah resistor seperti Gambar 2
Gambar 2. Rangkaian R, Bentuk Phasor, dan
Bentuk Gelombang Pada AC
Persamaan tegangan sumber
v = Vm Sin ωt
Persamaan tegangan pada Resistor R
v = i R
v = tegangan sesaat
i = arus sesaat
R = resistansi
Sehingga i = 
i = Im Sin ωt
Pada beban resistor murni tegangan dan arus mempunyai fasa sama (sefase).
Daya sesaat ( p )
P = vi = Vm Sin ωt .Im Sin ωt
= Vm Im Sin 2 ωt
= 
= 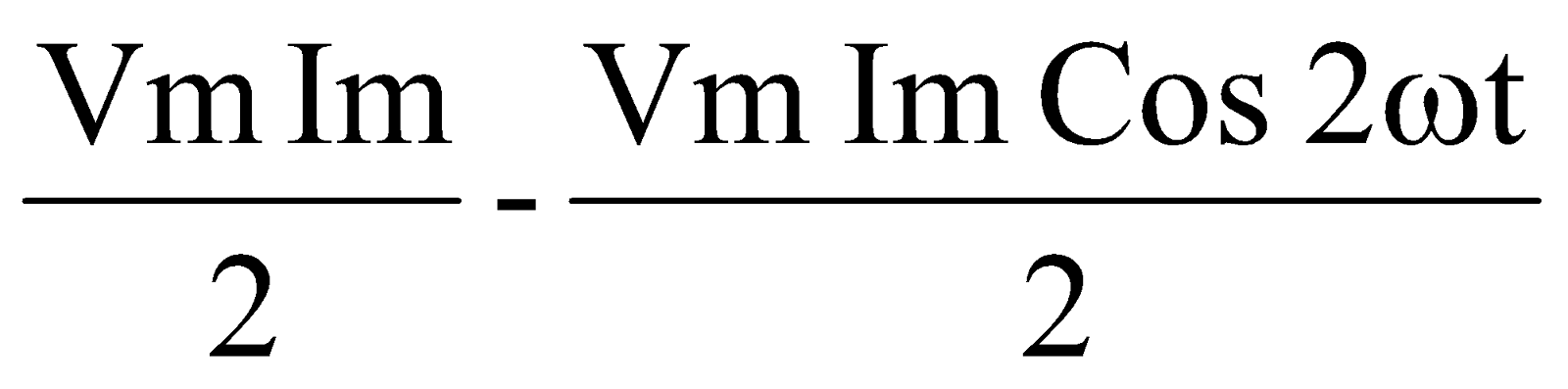
Untuk satu gelombang nilai rata – rata
sehingga daya
P =
Atau
P = V I watt
V = Tegangan Efektif
I = Arus Efektif
b.Induktor murni dalam arus bolak – balik
Bila tegangan bolak – balik dipasang pada induktor murni seperti Gambar 3 di bawah, maka induktor menghasilkan ggl yang melawan sumber yang besarnya
V = L
L

Gambar 3. Rangkaian L dan Bentuk Pashor Pada AC.
Tegangan Sumber
v = Vm Sin ωt
sehingga
Vm Sin ωt = L
Arus sesaat ( i ) maksimum Im =  jika
jika  mempunyai nilai 1maka persamaan arus pada Induktor menjadi
mempunyai nilai 1maka persamaan arus pada Induktor menjadi
I = Im 
Arus ketinggalan dengan sudut 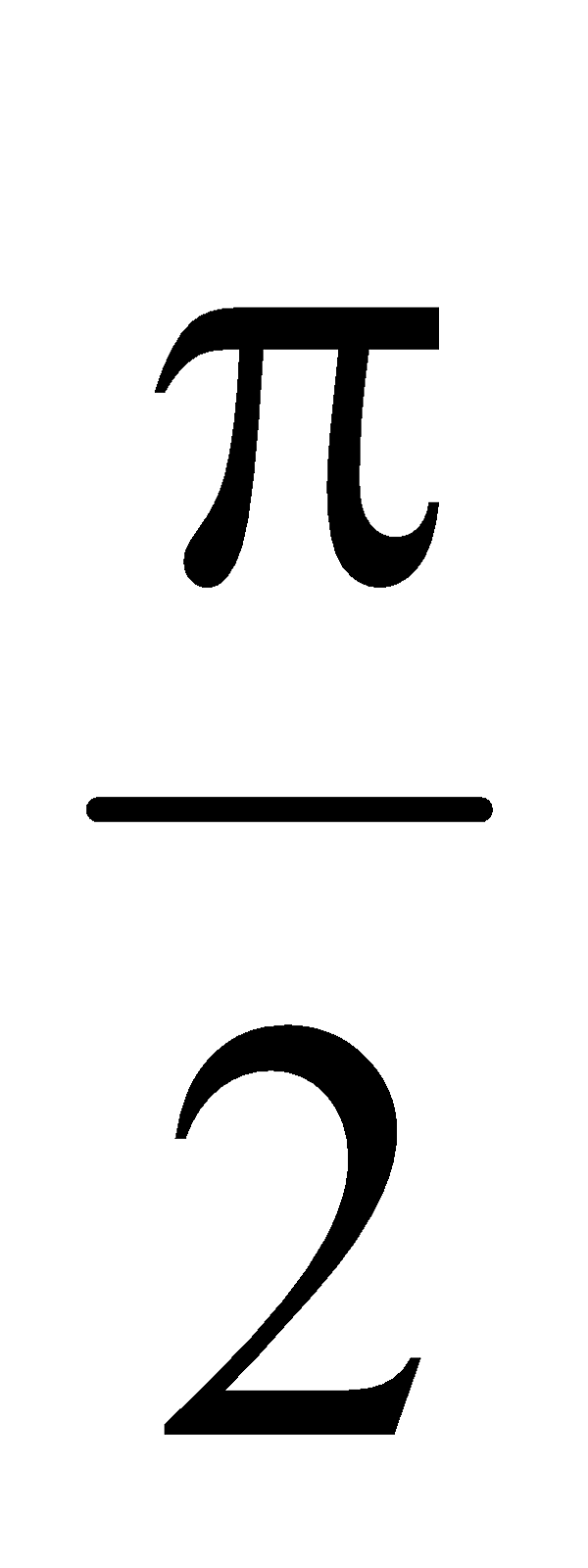 atau 90o .
atau 90o .
Daya Sesaat
Bentuk gelombang tegangan dan arus pada induktor dapat dilihat dalam Gambar 4 berikut ini.
Gambar 4. Bentuk Gelombang Tegangan dan Arus Pada Induktor
P = vi
= Vm Im Sin ωt 
p = daya sesaat
Daya Untuk seluruh siklus
P = -
Dari persamaan di atas dapat dijelaskan bahwa induktor murni tidak menyerap daya listrik hanya menyimpan energi listrik sesaat dalam jumlah terbatas.
b.Kapasitor dalam arus bolak – balik
Rangkaian yang terdiri dari sebuah sumber tegangan bolak – baliik dan sebuah kapasitor.
Gambar 5 di bawah.
IC

VC
Tegangan sumber mempunyai persamaan
v = Vm 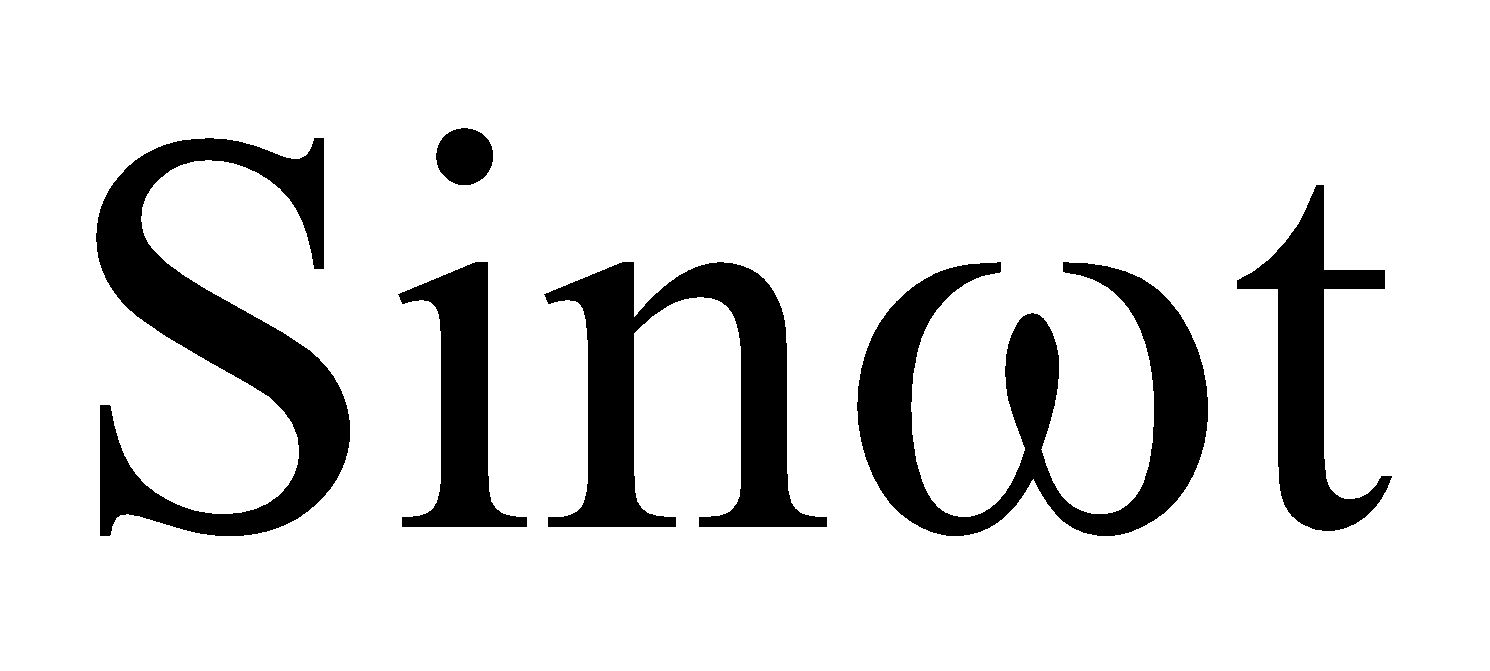
Muatan pada kapasitor
q = Cv
q = Muatan pada plat kapasitor
C = Kapasitansi kapasitor
V = Beda potensial/tegangan
Persamaan Arus
Dari persamaan tersebut terlihat bahwa arus mendahului tegangan dengan sudut 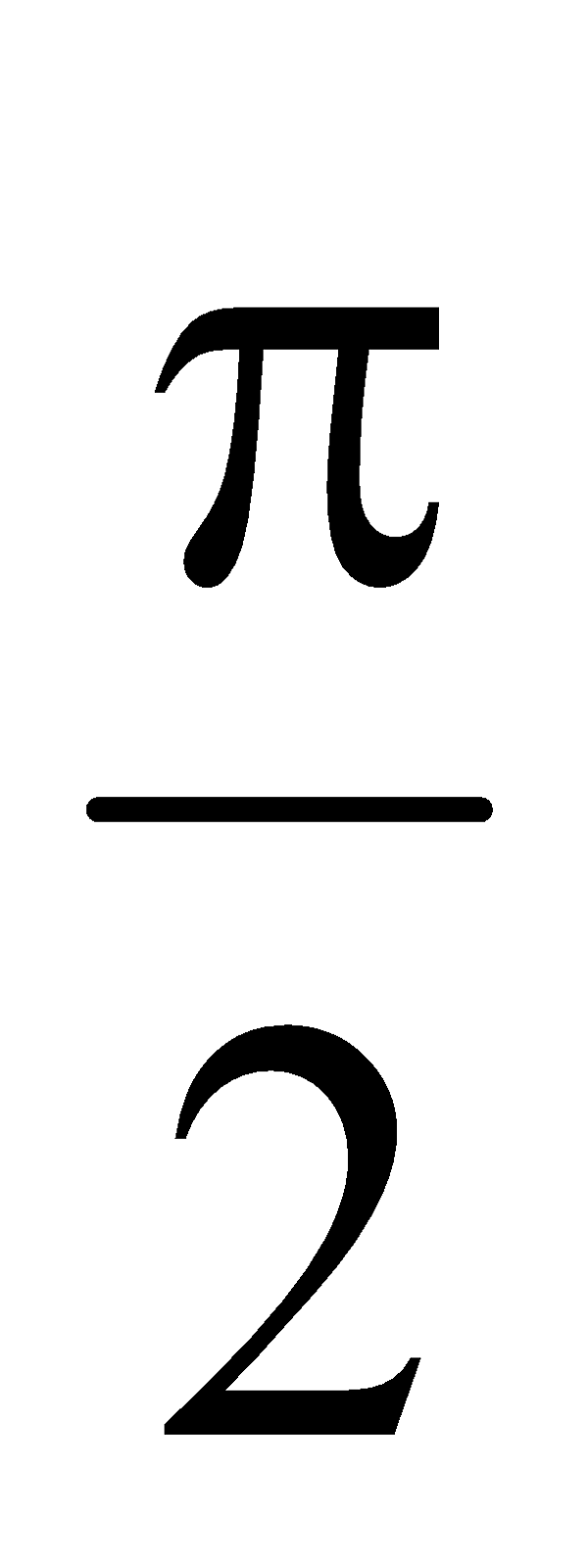 atau 900
atau 900
Daya
Daya sesaat pada kapasitor ( p )
P = vi
= Vm 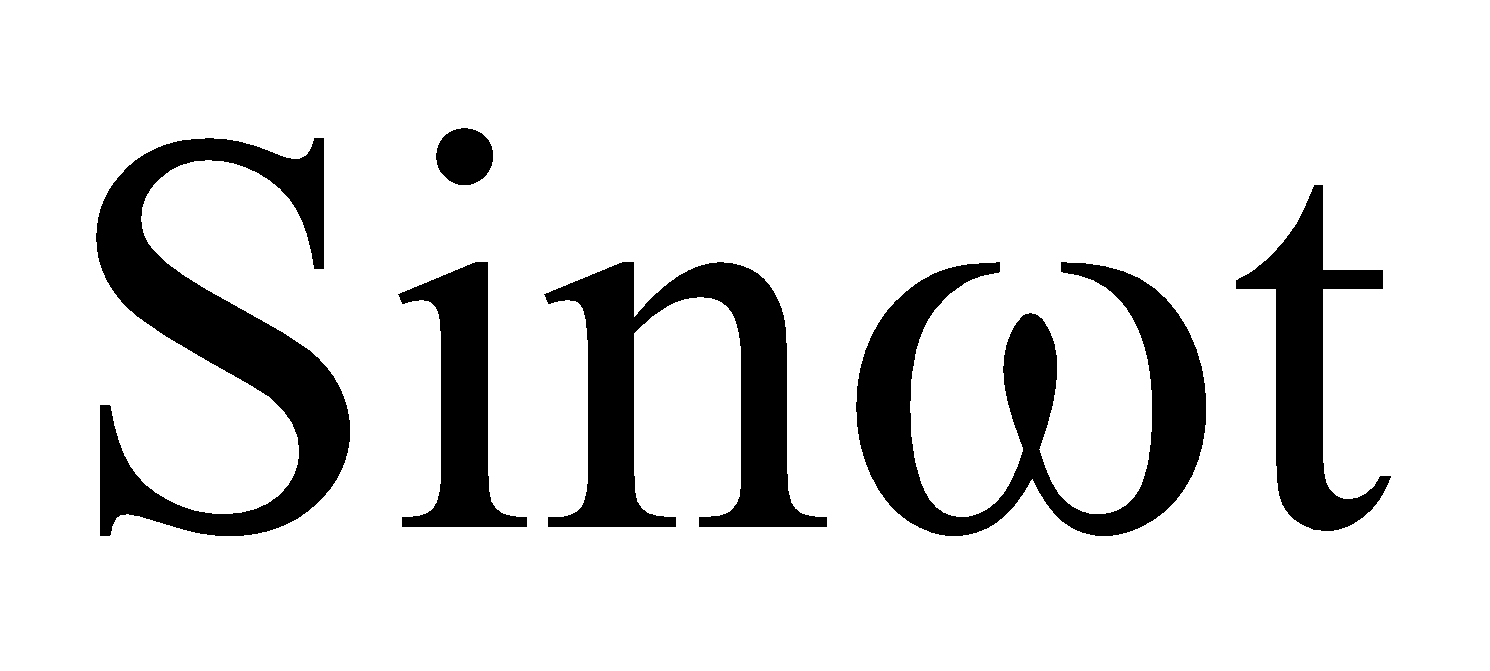

= Vm Im 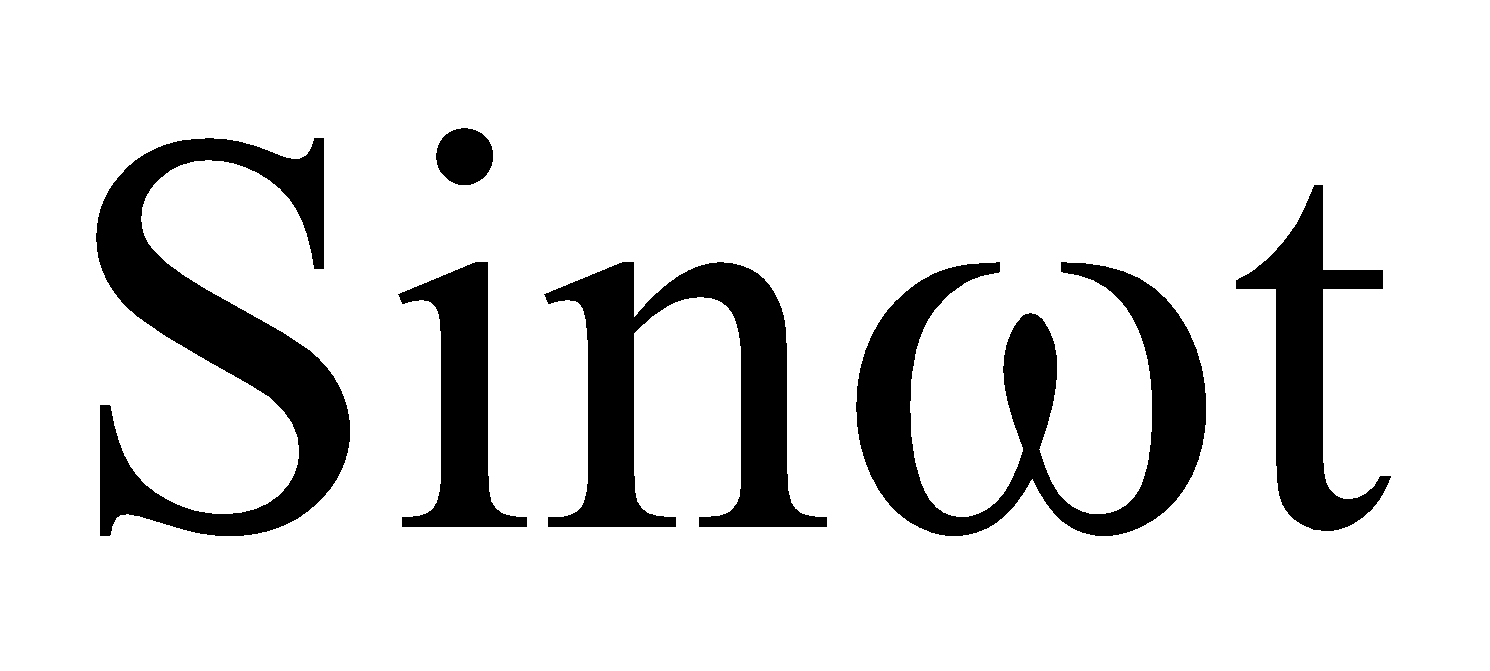

=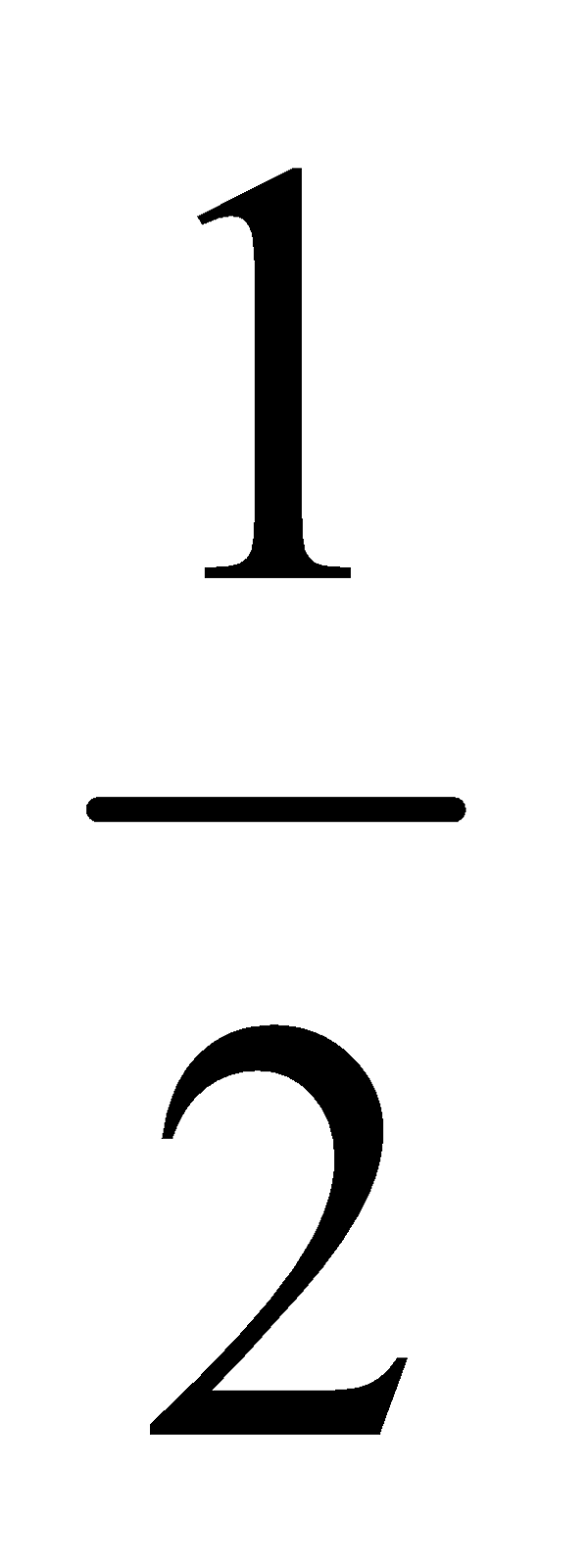 Vm Im
Vm Im 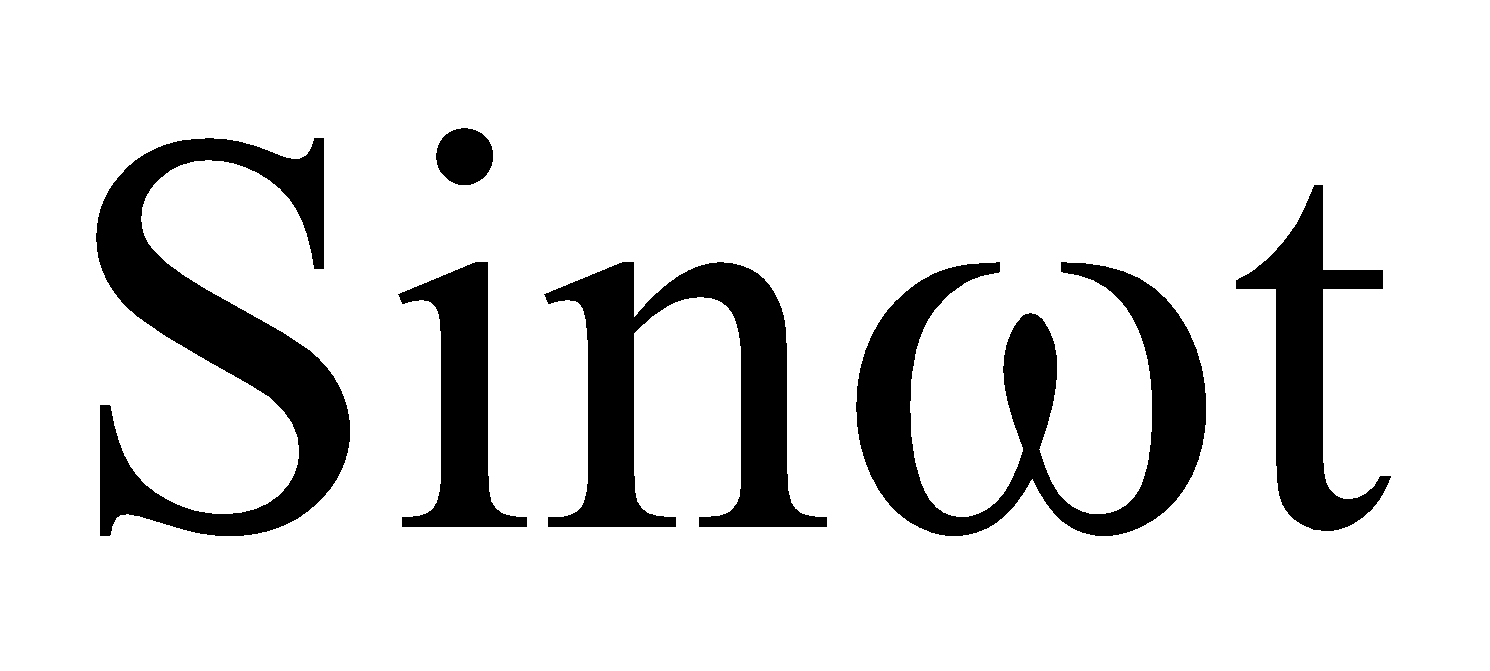
daya untuk seluruh siklus
P = 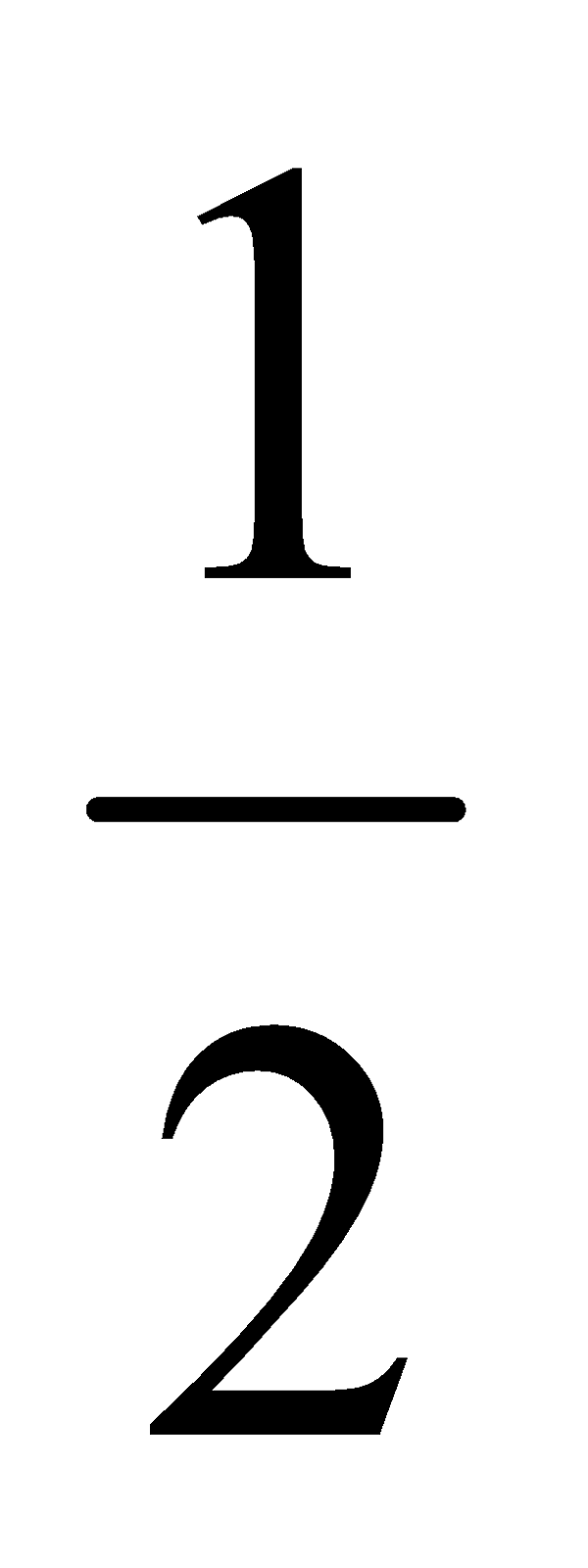 Vm Im
Vm Im 
Tabel 1. Karakteristik tegangan dan arus R, L, dan C
Elemen
|
Sudut fasa arus
Dan tegangan
|
Diagram
|
Impedansi
|
R
L
C
|
Fasa sama
Arus ketinggalan 900 atau ½ π
Arus mendahului tegangan900 atau ½ π
|
R
XL= ωL = 2π
XC =
|
B.ALJABAR PHASOR
1.Fungsi Pemaksa Kompleks
Disini akan dibahas penggunaan sebuah fungsi pemaksa kompleks ( fungsi pemaksa yang mempunyai bagian riel dan imjiner ) kepada sebuah rangkaian listrik. Hal ini mungkin kelihatannya aneh, akan tetapi akan diperoleh bahwa penggunaan kuantitas kompleks di dalam analisis “ keadaan mantap sinusoida “ menghasilkan metoda yang jauh lebih sederhana daripada metoda yang hanya menyangkut kuantitas riel.
Diharapkan fungsi pemaksa kompleks akan menghasilkan respons kompleks dengan suatu asumsi yang benar bahwa :
- bagian riel fungsi pemaksa akan menghasilkan bagian riel dari respon
- bagian imajiner fungsi pemaksa akan menghasilkan bagian imajiner dari respon.
Untuk membuktikan kebenaran dari asumsi ini, tinjau sebuah rangkaian pada gambar 1, yang menunjukkan : 
sebuah sumber atau fungsi pemaksa sinusoida :
Vm cos ( ωt + θ ) ……………….( 9-1 )
dihubungkan pada sebuah rangkaian N yang dianggap pasif, dan kemudian akan ditentukan respons arus , yang juga merupakan sinusoida keadaan mantap :
Im cos ( ωt + ø ) ………………..( 9-2 )
Kemudian, referensi waktu diubah dengan menggeser fasa atau sudut fasa fungsi pemaksa sebesar 900 atau mengubah saat t = 0, maka fungsi pemaksa menjadi :
Vm cos ( ωt + θ - 900 ) = Vm sin ( ωt + θ ) ………………..( 9-3 )
fungsi pemaksa pada persamaan ( 9-3 ), jika digunakan pada rangkaian yang sama akan menghasilkan respons :
Im cos ( ωt + ø - 900 ) = Im sin ( ωt + ø ) ………………..( 9-4 )
Selanjutnya, menyimpang dari realitas fisis, akan digunakan sebuah fungsi pemaksa imajiner, yang tidak dapat diterapkan di laboratorium, tetapi dapat digunakan secara matematis.
Untuk membuat sebuah fungsi sumber imajiner cukup dengan mengalikan fungsi pemaksa pada persamaan ( 9-3 ) dengan sebuah operator imajiner ” j “, sehing-ga diperoleh :
j Vm sin ( ωt + θ ) ………………..( 9-5 )
Prinsip linieritas menyatakan : jika sebuah sumber dilipatduakan, maka respons-nya juga akan dilipatduakan.
Berdasarkan prinsip linier, perkalian fungsi pemaksa ( sumber ) dengan sebuah konstanta k akan menghasilkan perkalian respons paksaan oleh konstanta k yang sama.
Jadi, respons dari sumber imajiner pada persamaan ( 9-5 ) adalah :
j Im sin ( ωt + ø ) ………………..( 9-6 )
Pada gambar 2, ditunjukkan fungsi pemaksa imajiner dan respons 
Jadi, fungsi pemaksa kompleks adalah jumlah dari fungsi pemaksa yang dinyatakan dalam persamaan ( 9-1 ) dan ( 9-5 ), yaitu :
Vm cos ( ωt + θ ) + j Vm sin ( ωt + θ ) ………………..( 9-7 )
haruslah menghasilkan repons paksaan kompleks, yang merupakan jumlah respons yang dinyatakan dalam persamaan ( 9-2 ) dan ( 9-6 ), yaitu :
Im cos ( ωt + ø ) + j Im sin ( ωt + ø ) ………………..( 9-8 )
Sumber dan respons kompleks dapat dinyatakan dengan menggunakan identitas Euler, jadi sumber pada persamaan ( 9-7 ), menjadi :
Vm e j ( ωt + θ ) ………………..( 9-9 )
dan respons pada persamaan ( 9-8 ) menjadi :
Im e j ( ωt + ø ) ………………..( 9-10 )
Pada gambar 3, ditunjukkan fungsi pemaksa kompleks ( sumber ) dan responsnya.
2. Fasor
Arus dan tegangan sinusoida pada suatu frekuensi yang diketahui, dicirikan oleh hanya dua parameter, yaitu :
- Ampiltudo dan
- Sudut fasa
Representasi kompleks dari tegangan dan arus juga dicirikan oleh kedua parameter yang sama.
Sebagai contoh : respons arus sinusoida : Im cos ( ωt + ø )
Representasi arus ini dalam bidang kompleks adalah : Im e j ( ωt + ø )
Jika Im dan ø sudah ditentukan, maka arus dapat didefinisikan dengan tepat.
Pada seluruh rangkaian linier yang bekerja dalam keadaan setimbang ( tunak ) sinusoida pada frekuensi tunggal ω, maka setiap arus dan tegangan dapat diberikan ciri secara lengkap, apabila amplitudo dan sudut fasanya diketahui.
Representasi kompleks dari setiap arus dan tegangan akan mengandung faktor e j ωt yang sama.
Kuantitas-kuantitas kompleks biasanya dituliskan dalam bentuk polar dan bukan dalam bentuk eksponensial, untuk menghemat waktu dan tenaga.
Contoh : tegangan sumber : v( t ) = Vm cos ωt, dinyatakan dalam bentuk kompleks sebagai : Vm 00 . 
dan arus respons : i( t ) = Im cos ( ωt + ø ), dinyatakan dalam bentuk kompleks sebagai : Im ø . 
Jadi, representasi kompleks yang disingkat ini disebut dengan Fasor.
3. Hubungan Fasor untuk R, L dan C
Disini dibahas hubungan antara tegangan dan arus fasor untuk elemen pasif R, L dan C, dan akan dimulai dengan persamaan untuk setiap elemen, mendefinisikan :
- hubungan daerah waktu
- membuat arus dan tegangan menjadi kuantitas kompleks
- menekan/menghilangkan e jωt dari persamaan, sehingga hubungan antara tegangan fasor dan arus fasor menjadi nyata.
Untuk rangkaian tahanan R ( Ohm atau Ω )
gambar 5a (dalam daerah waktu ) : persamaan yang mendefinisikan
v( t ) = R i( t ) …………..( 9-14 )
Tegangan kompleks : Vm e j ( ωt + θ ) = Vm cos ( ωt + θ ) + j Vm sin (ωt + θ ) ....( 9-15 )
Dengan anggapan bahwa arus kompleks :
Im e j ( ωt + ø ) = Im cos ( ωt + ø ) + j Im sin (ωt + ø ) ………….....( 9-16 )
Subsitusikan Persamaan ( 9-15 ) dan ( 9-16 ) kedalam persamaan ( 9-14 ), diperoleh :
Vm e j ( ωt + θ ) = R Im e j ( ωt + ø ) ………….....( C )
Ruas kanan dan kiri pada persamaan ( C ) dibagi dengan e j ωt :
Vm e j θ = R Im e j ø 

Atau dalam bentuk fasor : Vm θ = R Im ø

Vm θ dan Im ø , menyatakan fasor tegangan V dan fasor arus I, jadi :
V = R I ………….....( 9-17 )
Persamaan ( 9-17 ), menyatakan hubungan tegangan dan arus dalam bentuk fasor untuk sebuah tahanan, mempunyai bentuk yang sama seperti hubungan tegangan ada arus dalam daerah waktu.
Persamaan yang mendefinisikan bentuk fasor digambarkan pada gambar 5b ( daerah frekuensi ), dan sudut fasa θ = ø, sehingga tegangan dan arus sefasa.
Contoh : penggunaan hubungan daerah waktu dan daerah frekuensi
Sebuah tegangan v( t ) = 8 cos ( 100 t – 50 0 ) V, melintasi sebuah tahanan 4 Ω, dan bekerja di dalam daerah waktu, maka diperoleh besarnya arus :
v( t ) 8 cos ( 100 t – 50 0 )
i( t ) = ------ = ---------------------------- = 2 cos ( 100 t – 50 0 )
R 4
Bentuk fasor dari tegangan v( t ) = 8 cos ( 100 t – 50 0 ) adalah 8 - 500, sehingga arus fasor : 
V 8 - 500
I = ----- = ------------- = 2 - 500 A
R 4
Untuk Rangkaian Induktansi L ( Henry atau H )
Gambar 6a ( dalam daerah waktu ) :
v( t ) = L di/dt ….....( 9-18 )
Subsitusikan Persamaan ( 9-15 ) dan ( 9-16 ) kedalam persamaan ( 9-18 ), diperoleh :
Vm e j ( ωt + θ ) = L d/dt ( Im e j ( ωt + ø ) )
Vm e j ωt e j θ = j ω L Im e j ωt e j ø ( bagi dengan e j ωt ), diperoleh :
Vm e j θ = j ω L Im e j ø
Hubungan fasor yang diinginkan :
V = j ω L I ..………….....( 9-19 )
Persamaan daerah waktu ( 9-18 ) berubah menjadi persamaan ( 9-19 ) dalam daerah frekuensi, dengan bentuk fasor ditunjukkan pada gambar 6b.
Dari persamaan ( 9-19 ), dapat dilihat faktor j ω L berada pada + 900 ( ω L 900 ), dan didalam sebuah induktor arus I menyusul ( lagging ) terhadap tegangan V sebesar 900. 
Contoh : sebuah tegangan sebesar 8 - 500 V, dengan frekuensi ω = 100 rad/det
mensuplai sebuah induktor L = 4 H, maka besar arus fasor adalah :
V 8 - 500

I = ------ = -------------- = - j 0,02 - 500 = 0,02 - 1400 A
j ω L j 100 x 4
jadi, besar arus didalam daerah waktu adalah :
i( t ) = 0,02 cos ( 100 t - 1400 ) A
Untuk Rangkaian Kapasitansi C ( Farad atau F )
Gambar 7a ( dalam daerah waktu :
i( t ) = C dv/dt .....( 9-20 )
Subsitusikan Persamaan ( 9-15 ) dan ( 9-16 ) kedalam persamaan ( 9-20 ), diperoleh :
Im e j ( ωt + ø ) = C d/dt ( Vm e j ( ωt + θ ) )
Im e j ωt e j ø = j ω C Vm e j ωt e j θ ( dibagi dengan e j ωt ) , diperoleh :
Im e j ø = j ω C Vm e j θ
Hubungan fasor yang diinginkan :
I = j ω C V ..………….....( 9-21 )
Persamaan daerah waktu ( 9-20 ) berubah menjadi persamaan ( 9-21 ) dalam daerah frekuensi, dengan bentuk fasor ditunjukkan pada gambar 7b.
Dari persamaan ( 9-21 ), dapat dilihat faktor j ω C berada pada + 900 ( ω C 900 ), dan didalam sebuah kapasitor arus I mendahului ( leading ) terhadap tegangan V sebesar 900.
Contoh : sebuah tegangan fasor 8 - 500 mensuplai sebuah kapasitor 4 F, dengan w = 100 rad/det, maka besar arus fasor adalah :


I = j 400 x 4 x 8 - 500 = 3200 - 500 + 900 = 3200 400 A
jadi, besar arus didalam daerah waktu adalah :
i( t ) = 3200 cos ( 100 t + 400 ) A
Hubungan untuk ketiga elemen pasif sudah diperoleh, dan hasilnya disimpulkan pada tabel.
Tabel 1: Perbandingan dan ikhtisar hubungan antara v dan i dalam daerah waktu dan V dan I dalam daerah frekuensi untuk R, L, dan C
Daerah Waktu
|
Daerah Frekuensi
| ||
v = R i
v = L di/dt
v = 1/C ∫ i dt
|
V = R I
V = j ω L I
V = ( 1 / j ω C ) I
= - j / ωC
| ||
Dari tabel 1, semua persamaan fasor adalah persamaan aljabar dan setiap persamaan adalah linier, dan persamaan yang menghubungkan induktansi dan kapasitansi mempunyai banyak kesamaan dengan hukum ohm, dan akan menggunakannya sebagaimana menggunakan hukum ohm.
Contoh : Penggunaan konsep fasor, dengan meninjau kembali rangkaian RL seri yang telah beberapa kali ditinjau sebelumnya.
Dari gambar dapat dilihat bahwa seluruh besaran telah dinyatakan dalam daerah frekuensi.
Respons arus dalam daerah waktu dapat diperoleh, dengan terlebih dahulu menghi- tung arus fasor.
Dengan menerapkan hukum tegangan Kirchhoff, diperoleh :
VR + VL = Vs ( R + j ω L ) I = Vs, jadi arus fasor :
Vs Vm 00 Vm
I = ------------ = ----------------------------------------- = ------------------ tan - 1 ( ω L / R
R + j ω L √ R2 + ω2 L2 tan - 1 ( ω L / R ) √ R2 + ω2 L2 

Vm
Jadi arus dalam daerah waktu : i( t ) = --------------- cos ( ω t - tan - 1 ( ω L / R )
√ R2 + ω2 L2
Arus i( t ) diatas sama dengan yang diperoleh pada pembahasan terdahulu, yang menggunakan cara yang lebih rumit.
H. Impedansi ( Z ) dan Admitansi ( Y )
Impedansi ( Z )
Impedansi didefinisikan sebagai : Perbandingan antara tegangan fasor dengan
arus fasor, atau secara matematis :
Z = V / I ( ohm atau Ω )
Hubungan arus dan tegangan untuk ketiga elemen pasif didalam daerah frekuensi :
V = R I V = j ω L V = I / (j ω C )
Jika persamaan-persamaan diatas, dituliskan sebagai perbandingan antara tegangan fasor dan arus fasor, diperoleh impedansi untuk R, L dan C, yaitu :
ZR = V / I = R ; ZL = V / I = j ω L ; ZC = V / I = 1 / ( j ω C ) = - j (1 / ω C)
Impedansi :
- diberi symbol Z, dan merupakan sebuah kuantitas kompleks dengan satuan ohm ( Ω ).
- bukan merupakan suatu fasor dan tidak dapat ditransformasikan kedalam daerah waktu, dengan mengalikan e jωt dan mengambil rielnya.
- bagian dari daerah frekuensi dan bukan merupakan bagian daerah waktu
- dapat dikombinasikan secara seri dan paralel, dengan hukum-hukum yang sama seperti pada tahanan.
Contoh : Untuk harga ω = 104 rad/det, sebuah induktor 5 mH yang dihubung seri dengan kapasitor 100 μF, dapat diganti dengan sebuah impedansi yang merupakan jumlah impedansi individu.
ZL = j ω L = j 10 4 x 5 . 10 - 3 = j 50 Ω
ZC = 1 / ( j ω C ) = - j / ( ω C ) = - j / (10 4 x 100 . 10 – 6 ) = - j 1 Ω
Zeq = ZL + ZC = j 50 – j 1 = j 49 Ω
Kombinasi parallel dari kedua elemen diatas pada ω = 10 4 rad/det
ZL ZC ( j 50 ) ( - j 1 ) 50
Zeq = ----------- = -------------------- = ------ = - j 1,02 Ω
ZL + ZC j 50 – j 1 j 49
Bentuk umum dari sebuah impedansi adalah :
Dalam bentuk polar : Z = | Z | φ
Dalam bentuk siku-siku : Z = R + j X
dimana : R = komponen penahan, merupakan bagian riel dari impedansi
X = komponen reaktif, merupakan bagian imajiner dari impedansi
Penerapan Konsep Impedansi untuk menganalisis Rangkaian
Tinjau rangkaian RLC didalam daerah waktu dan diinginkan respons daerah waktu, seperti ditunjukkan pada gambar 8a, akan tetapi analisis dilakukan dalam daerah frekuensi.
Ditanya : i( t )
Penyelesaian : Karena analisis dilakukan di dalam daerah frekuensi, maka rangkaian daerah frekuensi harus digambarkan terlebih dahulu ( gambar 8b ).
Sumber tegangan diubah ke daerah frekuensi :
v( t ) = 40 sin 3000 t = 40 cos ( 3000 t - 900 ) V = 40 - 900 V
Respons arus i( t ) menjadi I
ZL = j ω L = j 3000 x 1/3 = j 1000 Ω = j 1 KΩ
ZC = 1 / ( j ω C ) = 1 / ( j 3000 x 1/6 .10 - 6 = - j / ( 0,5 10 - 3 ) = - j 2 KΩ
Rangkaian daerah frekuensi :
j 1 ( 1 – j 2 ) 2 + j 1
Zeq = 1,5 + ----------------- = 1,5 + --------
j 1 + 1 – j 2 1 – j 1
2 + j 1 1 + j 1
= 1,5 + --------- x -------
1 – j 1 1 + j 1
1 + j 3 
Zeq = 1,5 + --------- = 2 + j 1,5 KΩ = 2,5 36,90 KΩ
2
V 40 - 900

Arus fasor I adalah : I = ------- = ----------------- = 16 - 900 - 36,90 = 16 -126,90 mA
Z 2,5 36,90
Jadi arus dalam daerah waktu adalah :
i( t ) = 16 cos ( 3000 t – 126,90 ) mA
Admitansi ( Y )
Admitansi didefinisikan sebagai: Perbandingan antara arus fasor dengan tegangan fasor, atau secara matematis :
Y = I / V ( mho atau 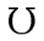 ), jadi Y = 1 / Z atau Z = 1 / Y
), jadi Y = 1 / Z atau Z = 1 / Y
Hubungan arus dan tegangan untuk ketiga elemen pasif didalam daerah frekuensi :
V = R I V = j ω L V = I / ( j ω C )
Jika persamaan-persamaan diatas, dituliskan sebagai perbandingan antara tegangan fasor dan arus fasor, diperoleh impedansi untuk R, L dan C, yaitu :
YR = I / V = 1 / R = G ; YL = I / V = 1 / ( j ω L) = - j ( ω L ) ; YC = I / V = j ω C
Admitansi :
- diberi symbol Y, dan merupakan sebuah kuantitas kompleks dengan satuan mho (
).
- bukan merupakan suatu fasor dan tidak dapat ditransformasikan kedalam daerah waktu, dengan mengalikan e jωt dan mengambil rielnya.
- bagian dari daerah frekuensi dan bukan merupakan bagian daerah waktu
- dapat dikombinasikan secara seri dan paralel, dengan hukum-hukum yang sama seperti pada tahanan.
Bentuk umum dari sebuah admitansi adalah :
Dalam bentuk polar : Y = | Y | φ
Dalam bentuk siku-siku : Y = G + j B = 1 / Z = 1 ( R + j X ) ………..( 9-22 )
dimana : G = komponen konduktansi, merupakan bagian riel dari admitansi
X = komponen suseptansi, merupakan bagian imajiner dari admitansi
Persamaan ( 9-22 ) tidak mengatakan bahwa bagian riel admitansi sama dengan kebalikan dari bagian riel impedansi, atau bagian imajiner admitansi sama dengan kebalikan bagian imajiner dari impedansi
Contoh : Jika sebuah impedansi Z = 1 – j 2 , maka admitansi Y adalah ;
1 1 1 1 + j 2
Y = ----- = --------- = --------- --------- = 0,2 + j 0,4 mho
Z 1 – j 2 1 – j 2 1 + j 2
C.RANGKAIAN SERI ARUS BOLAK-BALIK RLC
1. Rangkaian RL, RC, LC dan RLC
Rangkaian RL, RC, LC dan RLC merupakan gabungan antara resistor, induktor dan/atau kapasitor yang disusun secara seri. sebelum membahas lebih lanjut keempat jenis rangkaian di atas, perlu diketahui terlebih dahulu bahwa arus dan tegangan yang digunakan merupakan arus efektif (Ief) dan tegangan efektif (Vef). sedangkan pada rangkaian resesif, induktif dan kapasitif murni pada pembahasan sebelumnya menggunakan arus dan tegangan maksimal.
Arus Efektif Sumber
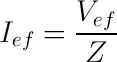
Arus Efektif Sumber
Z = impedansi rangkaian (ohm)
Rumus impedansi rangkaian (Z) akan dibahas pada tiap-tiap jenis rangkaian di atas. Jika besarnya arus efektif telah diketahui maka besarnya tegangan tiap-tiap komponen dapat dicari dengan rumus-rumus :
Keterangan :
VR = tegangan pada komponen resistor (V)
VL = tegangan pada komponen induktor (V)
VC = tegangan pada komponen kapasitor (V)
VR = tegangan pada komponen resistor (V)
VL = tegangan pada komponen induktor (V)
VC = tegangan pada komponen kapasitor (V)
a. Rangkaian Seri R-L
Setelah diketahui besarrrnya impedansi rangkaian (Z) maka dapat kita cari besarnya arus efektif (Ief) atau tegangan efektif (Vef). hubungan antara tegangan efektif dan tegangan antar komponen sebagai berikut :
ingat besarnya tegangan (V) yang diperoleh dari rumus di atas = tegangan efektif (Vef)
dan besarnya sudut fase rangkaian :
dan besarnya sudut fase rangkaian :
setelah diketahui besar tan dari sudut fase maka besar sutt fasenya dapat dicari.
b. Rangkaian Seri R-C
besarnya tegangan efektif :
dan besarnya sudut fase rangkaian :
c.Rangkaian Seri L-C
Rumus pada rangkaian ini lebih sederhana, yang penting terpenuhi syarat-syaratnya :
Rumus pada rangkaian ini lebih sederhana, yang penting terpenuhi syarat-syaratnya :
dan besarnya impedansi rangkaian (Z) :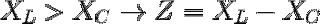
d. Rangkaian Seri R-L-C
Rangkaian ini merupakan rangkaian yang terlengkap komponenya, yakni terdapat resistor, induktor dan kapasitor. Sekaligus merupakan bentuk umum dari rumus-rumus dalam rangkaian yang dibahas sebelumnya. Artinya cukup menghafal dan memahami rumus-rumus dalam rangkaian ini maka rumus-rumus pada ketiga jenis rangkaian yang dibahas sebelumnya menjadi lebih paham dan tidak perlu dihafalkan.
impedansi rangkaian :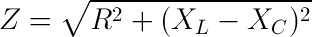
Rangkaian ini merupakan rangkaian yang terlengkap komponenya, yakni terdapat resistor, induktor dan kapasitor. Sekaligus merupakan bentuk umum dari rumus-rumus dalam rangkaian yang dibahas sebelumnya. Artinya cukup menghafal dan memahami rumus-rumus dalam rangkaian ini maka rumus-rumus pada ketiga jenis rangkaian yang dibahas sebelumnya menjadi lebih paham dan tidak perlu dihafalkan.
impedansi rangkaian :
tegangan efektif rangkaian :
sudut fase rangkaian :
Cara penggunaan rumus-rumus dalam rangkaian R-L-C untuk jenis rangkaian lainnya :
* Dalam rangkaian R-L tidak ada komponen kapasitor (C) maka nilai Xc dan Vc nya = nol (0).
*Dalam rangkaian R-C tidak ada komponen induktor (L) maka nilai XL dan VL nya = nol (0).
*Dalam rangkaian L-C tidak ada komponen resistor (R) maka nilai R dan VR nya = nol (0).
D.RANGKAIAN PARALEL ARUS BOLAK-BALIK RLC
1.RANGKAIAN RLC PARALEL
Rangkaian R-L-C paralel , sifat dari rangkaian paralel adalah terjadi percabangan arus dari sumber (i) menjadi tiga, yaitu arus yang menuju arus yang menuju resistor (iR), induktor (iL) dan kapasitor (iC). Sedangkan tegangan jatuh pada resistor (vR), pada induktor (vL) dan pada kapasitor (vC) sama besar dengan sumber tegangan (v). Gambar rangkaian R-L-C parallel dibawah memperlihatkan hubungan arus secara vektoris pada rangkaian R-L-C paralel.
Suatu rangkaian arus bolak-balik yang terdiri dari resistor (R), reaktansi induktif (XL) dan reaktansi kapasitif (XC), dimana ketiganya dihubungkan secara paralel. Fasor tegangan (v) sebagai sumber tegangan total diletakan pada ωt = 0. Arus efektif (iR) berada sefasa dengan tegangan (v). Arus yang melalui reaktansi induktif (iL) tertinggal sejauh 900 terhadap tegangan (v) dan arus yang melalui reaktansi kapasitif (iC) mendahului sejauh 900 terhadap tegangan (v).
Arus reaktif induktif (iL) dan arus reaktif kapasitif (iC) bekerja dengan arah berlawanan, dimana selisih dari kedua arus reaktif tersebut menentukan sifat induktif atau kapasitif suatu rangkaian. Arus gabungan (i) adalah jumlah geometris antara arus efektif (iR) dan selisih arus reaktif (iS) yang membentuk garis diagonal empat persegi panjang yang dibentuk antara arus efektif (iR) dan selisih arus reaktif (iS). Posisi arus (i) terhadap tegangan (v) ditentukan oleh selisih kedua arus reaktif (iS).
Bila arus yang melalui reaktansi induktif (iL) lebih besar daripada arus yang melalui reaktansi kapasitif (iC), maka arus total (i) tertinggal sejauh 900 terhadap tegangan (v), maka rangkaian paralel ini cenderung bersifat induktif. Sebaliknya bilamana arus yang melalui reaktansi induktif (iL) lebih kecil daripada arus yang melalui reaktansi kapasitif (iC), maka arus total (i) mendahului sejauh 900 terhadap tegangan (v), maka rangkaian paralel ini cenderung bersifat kapasitif. Untuk menghitung hubungan seri antara R, XL dan XC pada setiap diagram fasor kita ambil segitiga yang dibangun oleh arus total (i), arus.selisih (iS) dan arus efektif (iR). Dari sini dapat dibangun segitiga daya hantar, yang terdiri dari daya hantar resistor (G), daya hantar reaktif (B) dan daya hantar impedansi (Y).
Gambar Rangkaian R-L-C Paralel
Sehingga hubungan arus (i) terhadap arus cabang (iR), (iL) dan (iC) dapat ditentukan dengan menggunakan persamaan kuadrat berikut;
Sehingga
Oleh karena arus reaktif (iS) adalah selisih dari arus reaktif (iL) dan arus reaktif (iC), maka daya hantar reaktif (B) adalah selisih dari daya hantar reaktif (BL) daya hantar reaktif (BC).
dimana
B=BC-BL dan
impedansi (Z)
dengan arus total (i) = v . Y
Untuk arus pada hubungan paralel berlaku persamaan
Arus efektif iR = v . G
Arus reaktif induktif iL = v . BL
Arus reaktif kapasitif iC = v. BC
Sudut fasa (ϕ) dapat dihitung dari persamaan
B. IMPEDANSI R-L PARALEL
Gambar 1.6. Rangkaian R-L Paralel
Untuk menganalisa rangkaian paralel AC, perlu adanya pengetahuan mengenai analisa rangkaian paralel pada DC. Pada rangkaian paralel, tegangan yang jatuh pada masing-masing beban sama dengan tegangan sumber, sedangkan arus yang mengalir pada masing-masing beban tergantung pada nilai hambatannya.
Untuk komponen resistif, hambatannya harga resistansi, untuk komponen induktif, hambatannya harga reaktansi induktif dan untuk komponen kapasitif, hambatannya reaktansi kapasitif.
Untuk nilai impedansi dari rangkaian R-L paralel :
IMPEDANSI R-C PARALEL
Gambar 1.7. Rangkaian R-C Paralel
Untuk nilai impedansi dari rangkaian R-C paralel :
Besarnya arus yang melalui tiap tahanan akan berbeda sesuai dengan nilai tahanannya. Sedangkan beda potensialnya atau tegangan pada tiap masing-masing tahanan adalah sama dengan tegangan sumber.
Untuk tegangannya dapat dianalisis sesuai dengan cara sambungannya. Sambungan secara seri memiliki jumlah seluruh tegangan tiap tahanannya sama dengan tegangan sumber, sedangkan sambungan paralel tegangan setiap tahanannya sama besar.
E.RANGKAIAN POLY PHASE
Pada banyak aplikasi rangkaian, kita menemukan komponen- komponen yang terhubung bersama pada satu dari dua caraa sehingga membentuk rangkaian tiga terminal: sambungan “Delta” atau Δ(juga diketahui sebagai “pi” (π) dan juga sambungan “Y” (wye atau disebut juga “T”).
Hal ini dimungkinkan bagi kita untuk menghitung nilai resistor-resistor yang tepat untuk menggantikan bentuk ini (Y dan Δ) ke bentuk yang lainnya. Rangkaian Δ dan Y mempunyai sifat yang sama.
Gambar 1. Rangkaian Delta (Δ) dan Wye (Y)
Gambar 2. Rangkaian Tee (T) dan Pi (π)
Jika sekumpulan resistansi yang membentuk hubungan tertentu saat dianalisis ternyata bukan merupakan hubungan seri ataupun hubungan paralel yang telah kita pelajari sebelumnya, maka jika rangkaian resistansi tersebut membentuk hubungan star atau bintang atau rangkaian tipe Y, ataupun membentuk hubungan delta atau segitiga atau rangkaian tipe ∆, maka diperlukan transformasi baik dari star ke delta ataupun sebaliknya.
- Transformasi Dari Rangkaian Delta (∆) ke Rangkaian Wye (Y)
Perhatikan pada gambar di atas.
- Untuk mengubah Delta (∆) ke Wye (Y), hambatan titik A – C pada rangkaian delta harus sama dengan hambatan pada titik A – C rangkaian Wye (Y) sehingga didapat :
- Dengan cara yang sama, perhatikan titik B – C.
- Dengan cara yang sama, perhatikan titik A – B.
- Selanjutnya, kurangkan persamaan 3 dan 2
- Jumlahkan persamaan 1 dan 4
Sehingga dapat disimpulakan,, rumus untuk mengubah dari rangkaian Delta ke rangkaian wye adalah sebagai :
Catatan :
Persamaan diatas sangat dipengaruhi oleh posisi R pada gambar, jika pengindexan gambar diganti, maka persamaan harus disesuaikan dengan gambar yang baru.
- TRANSFORMASI DARI RANGKAIAN WYE KE RANGKAIAN DELTA
Berikut adalah cara mencari resistor pengganti untuk transformasi dari Rangkaian Wye ke Rangkaian Delta.
Dari transformasi Delta ke Wye diperoleh :
- Untuk memperoleh hubungan diperlukan mengkonversi dari suatu Y ke Δ, dengan cara membagi persamaan 7 dengan persamaan 5.
- Selanjutnya, membagi persamaan 7 dengan persamaan 6
- Subtitusikan persamaan 8,9 ke persamaan 6
Maka :
Sehingga dapat disimpulkan, rumus untuk mengubah dari rangkaian Wye ke rangkaian Delta adalah sebagai berikut :
CONTOH – CONTOH
- Rangkaian pada gambar di bawah ini, hitung RT, dan, I.
Penyelesaian:
- Konversikan “Y” menjadi “Δ” ekivalennya, karena tersambung “Y” memiliki nilai-nilai resistor sebesar
RΔ= 3 (10Ω) = 30Ω
Sehingga rangkainnya menjadi gambar di bawah ini.
- Selanjutnya, kita pralel kan 30Ω// 30Ω, 60Ω//30Ω serta 30Ω//90Ω
RP1= 30Ω . 30Ω30Ω+30Ω = 900Ω60Ω = 15Ω
RP2 = 60Ω . 30Ω60Ω+ 30Ω = 1800Ω90Ω = 20Ω
Rp3 = 30Ω . 90Ω30Ω+ 90Ω =2700Ω120Ω = 22,5Ω
Sehingga rangkaiannya menjadi gambar di bawah ini.
- Kita lihat sisi yang dihasilkan “Δ” adalah susunan paralel, sehingga nilai total resistansinya dapat dihitung dengan mudah
RT = RP1// (RP2 + Rp3)
RT = 15Ω .(20Ω+22,5Ω)15Ω+(20Ω+22,5Ω)
RT = 15Ω .42,5Ω15Ω+42,5Ω
RT = 637,5Ω5,75Ω
RT = 11,08Ω
Sehingga nilai arusnya adalah
I =VRT = I = 3011,08 = 2,7 Ampere
- Carilah nilai I dari rangkaian di bawah ini
Penyelesaian :
- Bila kita melihat resistor R1, R2,dan R3 sebagai suatu rangkaian Δ (pada rumus berturut-turut Rab, Rac, dan Rbc ) dan ingin menggantinya dengan rangkaian Y, kita bisa mengubah rangkaian jembatan ini menjadi rangkaia yang lebih sederhana yaitu rangkaian seri-paralel:
RA = R1 Rz R1+ Rz+ R3 RB = R1 R3 R1+ Rz+ R3 RB = RZ R3 R1+ Rz+ R3
= 6.9 6+9+12 = 6.9 6+9+12 = 9.12 6+9+12
RA = 5427 = 2Ω RB = 7227 = 2,67Ω RB = 108227 = 3Ω
Sekarang kita telah mendapatkan rangkaian yang lebih sederhana. Kita bisa menganalisa rangkaian ini menggunakan aturan seri – paralel:
- Serikan rangkaian RB dan R4 serta rangkaian Rc dan RB
RS1 = RB + R4
= 2,67Ω + 3Ω = 5,67 Ω
RS2 = RC + R5
RS2 = 3Ω + 6Ω = 9Ω
Sehingga terbentuk rangkaian seperti ini:
- Selanjutnya, hambatan RS1 dan RS2 diparalelkan
RS1// RS2 = RP
RP = RS1 . RSZRS1+ RSZ
Rp = 5,67.95,67+9 = 51,0314,67=3,47Ω
Dan terbentuk rangkain seri seperti ini:
- Dan rangkain di atas dihitung secara seri menjadi RT
RT = RA + RP
= 2 + 3,47 = 5,47 Ω
- Lalu, hitung I dengan menggunakan hukum Ohm
I = VRT
= 205,47=3,65 Ampere
F.HARMONIK.
1.PENGERTIAN
Harmonik adalah salah satu dari sekian banyak permasalahan yang menyangkut kualitas daya listrik. Keberadaan harmonik ini sangat mengganggu bahkan merugikan sistem apabila melebihi batas standar yang ditetapkan, dalam hal ini standar yang digunakan adalah standar IEEE 519-1992. Pada gambar 1. berikut akan diperlihatkan sebuah gelombang yang terdistorsi.
Gambar 1. Gelombang Terdistorsi Direpresentasikan dalam Deret Fourier
Harmonik Sumber Tegangan
Sumber tegangan yang dipakai dalam penelitian ini adalah trafo 3 fasa yang disuplay dari jaringan PLN. Tegangan sumber untuk inverter digunakan 220 volt antar fasa. Hasil pengukuran sampai dengan harmonik ke-10 diperlihatkan pada tabel 3., sedangkan untuk spektrum harmonik sampai dengan harmonik ke- 30 dapat dilihat pada gambar 3.
Tabel 3. Hasil pengukuran harmonik sumber tegangan
Gambar 2. Spektrum harmonik sumber tegangan
Pada gambar 3. dapat dilihat harmonik tertinggi terjadi pada fase S, yaitu harmonik ke-5. Nilai distorsi harmonik tegangan pada fasa R, S, dan T masing-masing adalah 2,494%, 2,794%, dan 2,546%. Sedangkan nilai total distorsi harmonik (THD) tegangan yang terukur masing-masing untuk fasa R, S, dan T adalah 2,614%, 2,861%, dan 2,595%. Menggunakan persamaan (1) diperoleh THD tegangan sumber pada fasa R sebesar 2,616%, pada fasa S sebesar 2,862%, dan pada fasa T sebesar 2,603%. Nilai ini masih berada di bawah standar IEEE 519-1992, yaitu 5% untuk tegangan sampai 69 kV. Jadi sumber tegangan ini masih bisa dipakai karena kandungan harmoniknya belum melebihi standar. Berikut adalah bentuk
gelombang tegangan sumber untuk masingmasing fasa.
Gambar 3. Gelombang tegangan sumber pada fasa R
2.HARMONIK
a. Sumber Harmonik pada Sistem Distribusi
Dalam sistem tenaga listrik dikenal dua jenis beban yaitu beban linier dan beban non linier. Beban linier adalah beban yang memberikan bentuk gelombang keluaran yang linier artinya arus yang mengalir sebanding dengan impedensi dan perubahan tegangan. Sedangkan beban non linier adalah bentuk gelombang keluarannya tidak sebanding dengan tegangan dalam setiap setengan siklus sehingga bentuk gelombang arus maupun tegangan keluarannya tidak sama dengan gelombang masukannya (mengalami distorsi). Beban non linier yang umumnya merupakan peralatan elektronik yang didalamnya banyak terdapat komponen semi konduktor, dalam proses kerjanya berlaku sebagai saklar yang bekerja pada setiap siklus gelombang dari sumber tegangan. Proses kerja ini akan menghasilkan gangguan atau distorsi gelombang arus yang tidak sinusoidal. Bentuk gelombang ini tidak menentu dan dapat berubah menurut pengaturan pada parameter komponen semi konduktor dalam peralatan elektronik. Perubahan bentuk gelombang ini tidak terkait dengan sumber tegangannya.
Beberapa peralatan yang dapat menyebabkan timbulnya harmonik antara lain komputer, printer, lampu fluorescent yang menggunakan elektronik ballast, kendali kecepatan motor, motor induksi, batere charger, proses eletroplating, dll. Peralatan ini dirancang untuk menggunakan arus listrik secara hemat dan efisien karena arus listrik hanya dapat melalui komponen semi konduktornya selama periode pengaturan yang telah ditentukan. Namun disisi lain hal ini akan menyebabkan gelombang mengalami gangguan gelombang arus dan tegangan yang pada akhirnya akan kembali ke bagian lain sistem tenaga listrik. Penomena ini akan menimbulkan gangguan beban tidak linier satu phase. Hal di atas banyak terjadi pada distribusi yang memasok pada areal perkantoran/komersial. Sedangkan pada areal perindustrian gangguan yang terjadi adalah beban non linier tiga phase yang disebabkan oleh motor listrik, kontrol keepatan motor, batere charger, electroplating, dapur busur listrik, dll.
b. Pengaruh Harmonik pada Komponen Sistem Distribusi
Setiap komponensistem distribusi dapat dipengaruhi oleh harmonik walaupun dengan akibat yang berbeda. Namun demikian komponen tersebut akan mengalami penurunan kinerja dan bahkan akan mengalami kerusakan. Salah satu dampak yang umum dari gangguan harmonik adalah panas lebih pada kawat netral dan transformator sebagai akibat timbulnya harmonik ketiga yang dibangkitkan oleh peralatan listrik satu phase. Pada keadaan normal, arus beban setiap phase dari beban linier yang seimbang pada frekuensi dasarnya akan saling mengurangi sehingga arus netralnya menjadi nol. Sebaliknya beban tidak linier satu phase akan menimbulkan harmonik kelipatan tiga ganjil yang disebut triplen harmonik (harmonik ke-3, ke-9, ke-15 dan seterusnya) yang sering disebut zero sequence harmonik (lihat Tabel 1). Harmonik ini tidak menghilangkan arus netral tetapi dapat menghasilkan arus netral yang lebih tinggi dari arus phase.
Tabel 1. Polaritas dari Komponen Harmonik
Harmonik
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Frequensi (Hz)
|
50
|
100
|
150
|
200
|
250
|
300
|
350
|
400
|
450
|
Uruan
|
+
|
-
|
0
|
+
|
-
|
0
|
+
|
-
|
0
|
Harmonik pertama urutan polaritasnya adalah positif, harmonik kedua urutan polaritasnya adalah negatif dan harmonik ketiga urutan polaritasnya adalah nol, harmonik keempat adalah positif (berulang berurutan sampai seterusnya).
Tabel 2. Akibat dari Polaritas dari Komponen Harmonik
Urutan
|
Pengaruh pada Motor
|
Pengaruh pada sistem distribusi
|
Positif
|
Menimbulkan medan magnet
putar arah majau (forward) |
Panas
|
Negatif
|
Menimbulkan medan magnet
putar arah mundur (reverse) |
Panas
Arah putaran motor berubah |
Nol
|
Tidak ada
|
Panas
Menimbulkan/menambah arus pada kawat netral |
Akibat yang dapat ditimbulkan oleh urutan polaritas komponen harmonik (lihat Tabel 2) antara lain tingginya arus netral pada sistem 3 phase 4 kawat (sisi sekunder transformator) karena arus urutan nol (zero sequence) dan arus ini akan terinduksi ke sisi primer transformator dan akan berputar pada sisi primer transformator yang biasanya memiliki belitan delta (D). Hal ini akibat pada kawat netral tidak memiliki peralatan pemutus arus untuk proteksi tegangan atau arus lebih. Pengaruh harmonik pada transformator sering tanpa disadari dan diantisipasi keberadaannya sampai terjadi gangguan yang penyebabnya tidak jelas. Hal ini dapat juga terjadi bila perubahan konfigurasi atau jenis beban yang dipasok. Transformator dan peralatan induksi lainnya, selalu terpengaruh oleh harmonik karena trafo itu sendiri dirancang sesuai dengan frekuensi kerjanya. selain itu transformator juga merupakan media utama antara pembangkit dengan beban.
Frekuensi harmonik yang lebih tinggi dari frekuensi kerjanya akan mengakibatkan penurunan efisiensi atau terjadi kerugian daya. Selain itu, ada beberapa akibat yang dapat ditimbulkan oleh adanya harmonik dalam sistem tenaga listrik, antara lain:
- Timbulnya getaran mekanis pada panel listrik yang merupakan getaran resonansi mekanis akibat harmonik arus frekuensi tinggi,
- Harmonik dapat menimbulkan tambahan torsi pada kWh meter jenis elektromekanis yang menggunakan piringan induksi berputar. Sebagai akibatnya, puratan piringan akan lebih cepat atau terjadi kesalahan ukur kWh meter karena piringan induksi tersebut dirancang hanya untuk beroperasi pada frekuensi dasar,
- Interferensi frekunsi pada sistem telekomunikasi karena biasanya kabel untuk keperluan telekomunikasi ditempatkan berdekatan dengan kawat netral. Triplen harmonik pada kawat netral dapat memberikan induksi harmonik yang mengganggu sistem telekomunikasi,
- Pemutusan beban. Pemutus beban dapat bekerja dibawah arus pengenalnya atau mungkin tidak bekerja pada arus pengenal. Pemutus beban yang dapat terhindar dari gangguan harmonik pada umumnya adalah pemutus beban yang mempunyai respon terhadap arus rms sebenarnya (true-rms current) atau kenaikan temperatur karena arus lebih.
c. Identifikasi Harmonik
Untuk mengidentifikasi kehadiran harmonik pada sistem distribusi, dapat diketahui melalui langkah-langkah sebagai berikut:
- Identifikasi Jenis Beban
Jenis beban yang dipasok, misalnya peralatan apa yang dipakai oleh konsumen. Bila banyaknya peralatan yang mempunyai komponen utama terbuat dari bahan semikonduktor seperti komputer dan alat bantunya, pengatur kecepatan motor, atau peralatan lain yang menggunakan arus searah maka dapat diperkirakan masalah harmonik ada diintalasi konsumen tersebut. - Pemeriksaan Transformator
Untuk transformator yang memasok beban non linier apakah ada kenaikan temperaturnya tidak normal. Arus sekunder transformator baik phase maupun netral perlu dilihat. Bandingkan arus netralnya dengan arus phase pada keadaan beban tidak seimbang. Apabila arus netralnya lebih besar maka dapat diperkirakan adanya trilen harmonik dan kemungkinan turunnya kinerja transformator.
- Pemeriksaan Tegangan Netral Tanah
Terjadinya arus lebih pada kawat netral (untuk sistem 3 phase dan 4 kawat) dapat diktahui dengan melihat tegangan netral-tanah pada keadaan berbeban. Apabila tegangan yang terukur lebih besar dari 2 Volt maka terdapat indikasi adanya masalah harmonik pada beban tersebut. Apabila indikasi-indikasi adanya harmonik telah diketahui maka perlu dilakukan langkah-langkah untuk mengatasi masalah gangguan harmonik antara lain dengan mengetahui harmonik untuk menentukan harmonik-harmonik yang dominan dan sumber utamanya.
Dampak Harmonik pada Sistem Instalasi Listrik dan Mitigasinya
A.Dampak Harmonik
Pergeseran sifat beban yang terjadi dalam selang waktu kira-kira limabelas tahun terakhir dalamkuantitas besar, yaitu dari beban linier ke beban nonlinier telah menimbulkan berbagai dampak yangberkaitan dengan introduksi harmonisa, yaitu inkompatibilitas peralatan, peningkatan rugi-rugi danpenurunan efisiensi sistem, penyimpangan sistem pengukuran dan analisis sistem tenaga,penurunan keandalan serta masalah policy / tanggung jawab.Berikut beberapa dampak harmonisa pada sistem instalasi lisrrik1.
Dampak Resonansi Paralel dan SeriResonansi paralel terjadi bilamana dipasang Kapasitor Kompensasi Daya Reaktif.Yaitu dimana arus harmonisa menghadapi suatu impedansi tinggi. Impedansi tinggi dapatdisebabkan oleh resonansi pada frekuensi harmonisa tersebut.
Salah satu cara yang dapat dilakukan untuk mengurangi pengaruh harmonik pada sistem distribusi adalah dengan mengurangi kapasitas suplai daya transformator (derating fransformator). Dalam menentukan besarnya pengurangan kapasitas transformator ada metode sederhana yang dapat dipergunakan yaitu dengan memakai persamaan sebagai berikut:
KVA baru = THDF x KVA pengenal ..................persamaan (1)
di mana THDF adalah Transformator Harmonic Derating Factor,
THDF = [1,414 x (arus phase rms) / (arus puncak phase sesaat)] x 100%
= [(1,414 x 1/3 x (Ir + Is + It)rms / 1/3 x (Ir + Is + It)puncak] x 100%
= [(1,414 x 1/3 x (Ir + Is + It)rms / 1/3 x (Ir + Is + It)puncak] x 100%
Impedansi rangkaian pararlel yang terdiri dari rangkaian paralel Ls, C dan R.Dimisalkan L adalah induktansi sistem yang dilengkapi dengan kapasitor kompensasi faktor dayaC. Apabila frekuensi resonansi jaringan paralel L dan C dekat dengan frekuensi arus harmonisaI maka dapat terjadi penguatan arus yang bersirkulasi antara L dan C. Arus osilasi yang tinggiini dapat menyebabkan terbangkitnya tegangan tinggi sehingga menimbulkan cacat tegangan dibus Point of Common Coupling (PCC).Persamaan impedansi adalah:Dengan mengabaikan R (tahanan beban linier), dimana:L = Induktansi suplai sistem (jaringan suplai, trafo dan konduktor)C = Kapasitansi kapasitor I = Arus harmonisaSesuai persamaan impedansi diatas, maka resonansi terjadi ketika persamaan 1-L-C cenderung rendah (nol), sehingga menghasilkan impedansi tinggi. Ketika arus melewatiimpedansi tinggi menimbulkan harmonisa tegangan yang dapat dilihat dari tingkat distorsitegangan.Resonansi juga dimungkinkan dengan komponen-komponen resonansi adalah induktansi sistem L dengan kapasitansi beban C ,L atau antara induktansi beban L (dari Z L) dengan kapasitorkompensasi C. Resonansi seri terjadi apabila sumber harmonisa menghadapi suatu impedansi rendah. Impedansiyang terbentuk dari induktansi saluran atau induktansi bocor transformator serta kapasitorkompensasi faktor daya berpeluang menimbulkan rangkaian resonan.
G.TRANSIENT.
Pada pembahasan rangkaian listrik, arus maupun tegangan yang dibahas adalah untuk ko ndisi steady state/mantap. Akan tetapi seb enarny a seb elum rangkaian mencapai keadaan steady state, arus maupun t egangan pada rangkaian menga lami transisi (transient), dan apabila transisi ini berakhir maka dikatakanlah arus maupun tegangan pada rangkaian tersebut telah mencapai keadaan steady state.
Adapun yang dibahas pada materi kuliah ini hanya mencakup rangkaia nrangkaian yang linear yang memiliki persamaan diferensial orde satu dan dua dengan konstanta sembarang.
1. Kondisi Awal
Dalam analisa rangkaian transient perlu dibedakan tiga daerah waktu yaitu:
1. Sesaat sebelum dilakukan perubahan pada rangkaian (pada kuliah ini yang dimaksudperubahan adalah posisi dari saklar pada rangkaian) yang dilambangkan pada saat t(0-).
2. Saat terjadinya perubahan yang dilambangkan pada saat t(0).
3. Sesaat setelah terjadinya perubahan y ang dilambangkan pada saat t(0+). Keadaan awal sangat diperlukan agar konstanta sembarang yang muncul dalam penyelesaian umum dari persamaan diferensial dapat dihitung.
Sebagaimana diketahui bahwa pen yelesaian umum suatu persamaa n difer ensial orde satu akan berisikan satu konstanta sembarang dan untuk persamaan diferensial orde dua akan berisikan dua buah konst anta sembara ng sedangka n untuk ord e n persamaa n diferensial akan memiliki n buah konstanta sembarang.
2. Kondisi Awal Komponen Rangkaian
Komponen R
Pada resistor ideal, arus dan tegangan dihubungkan dengan hukum Ohm V = IR, bila tegangan tegangan yang dikenakan pada resistor (unit step) aka arus akan mempunyai bentuk y ang sama dengan tegangan y ang hanya dirubah oleh faktor (1/R),maka dapat dikatakan bahwa arus y ang mengalir pada resistor akan segera berubah dengan seket ika bila tegangan pada terminal resistor tersebut dirubah, sehingga dapat dikatakan bahwa pada resistor :
iR(0-) ≠ iR(O) ≠ iR(0+)
Komponen L
Arus yang mengalir pada indu ktor tidak dapat berubah dengan seketika, karena energi yang secara tiba -tiba diberikan pada induktor tidak akan merubah arus yang ada sebelumnya pada induktor tersebu t, maka induktor akan bersifat sebagai rangkaian terbuka pada saat energi yang baru dikenakan pada inductor terseb ut, dengan demikian arus iL( 0 - ) yang mengalir akan tetap mengalir disaat terjadinya perubahan pada terminal induktor, atau dapat dikatakan
iL(0-) = iL(0) = iL(0+)
Komponen C
Tegangan pada kapasitor C yang memiliki kapasitansi tetap tidak dapat berubah dengan seketika, hal ini dapat dilihat dari bila sebuah kapasitor yang tidak
bermuatan dihubungkan ke sumber energi, maka arus akan mengalir dalam waktu
sesaat sehingga kapasitansi ekivalen dengan suatu rangkaian hubung singkat , hal ini
disebabkan tegangan dan muatan adalah berbanding lurus dalam kapasitor [v =q/c]
sehingga muatan nol sebanding dengan tegangan nol (sifat hubungan singkat).
Dengan muatan awal yang ada pada kapasitor, maka kapasitor ekivalen dengan
sebuah sumber tegangan sebesar [v0 = q0/c] dimana q0 adalah muatan awal.
Adapun sifat dari ketiga komponen tersebut secara ringkas dapat diperlihatkan
sebagai berikut :
H.KOMPONEN SIMETRIS.
1. Komponen Simetris
Metode komponen simetris digunakan untuk menguraikan suatu sistem tidak seimbang yang terdiri atas n buah fasor yang berhubungan menjadi n buah sistem fasor yang seimbang. Pada sistem tiga fasa, tiga fasor tidak seimbang dapat diuraikan menjadi tiga sistem fasor yang seimbang. Ketiga komponen seimbang pada komponen simetris adalah :
- Komponen urutan positif.
- Komponen urutan negatif.
- Komponen urutan nol.
- Komponen Urutan Positif
Komponen urutan ini terdiri dari tiga fasor yang sama besar, terpisah 1200 satu sama lain dan mempunyai urutan fasa yang sama dengan fasor aslinya. Gambar dibawah menunjukkan fasor komponen urutan positif dengan urutan fasa sistem tenaga listrik abc. Arah putaran fasor berlawanan dengan arah jarum jam.
Pada pergeseran sudut, akan lebih mudah menggunakan unit fasor dengan pergeseran sudut 1200 dalam arah yang berlawanan dengan arah jarum jam. Hal ini dinamakan sebagai operator fortescue,
Gambar Fasor tegangan urutan positif
Fasor tegangan urutan positif memiliki pola yang sama dengan fasor arus urutan positif, oleh karena itu pengaturan urutan positif dapat diperiksa kebenarannya sebagai berikut :
- Komponen Urutan Negatif
Komponen urutan ini terdiri dari tiga fasor yang sama besar, terpisah 1200 satu sama lain dan mempunyai urutan fasa yang berlawanan dengan fasor aslinya. Gambar dibawah menunjukkan fasor komponen urutan negatif dengan urutan fasa sistem tenaga listrik abc, maka urutan fasa komponen urutan negatif adalah acb. Arah putaran fasor berlawanan dengan arah jarum jam.
Gambar Fasor tegangan urutan negatif
Seperti halnya pada urutan positif, fasor tegangan urutan negatif memiliki pola yang sama dengan fasor arus urutan negatif, oleh karena itu pengaturan urutan negatif dapat diperiksa kebenarannya sebagai berikut :
- Komponen Urutan Nol
Komponen urutan ini terdiri dari tiga fasor yang sama besarnya dan dengan pergeseran fasa nol antara fasor yang satu dengan yang lain. Gambar di bawah ini menunjukkan fasor komponen urutan nol dengan urutan fasa sistem tenaga listrik abc.
Fasor tegangan urutan nol
Pengaturan tegangan dan arus urutan nol dapat diperiksa kebenarannya sebagai berikut :
Karena setiap fasor tak seimbang, yang asli adalah jumlah komponen, fasor asli yang dinyatakan dalam suku – suku komponennya adalah:
- Penurunan Menggunakan Matriks
Untuk memudahkan penghitungan, kita misalkan :
Maka kita peroleh :
Persamaan di atas menunjukkan bagaimana menguraikan tiga fasor tidak simetris menjadi komponen simetrisnya. Kita dapat menulis masing – masing persamaan di atas dalam bentuk biasa, kita peroleh :
Persamaan di atas menunjukkan bahwa tidak akan ada komponen urutan nol jika jumlah fasor tak seimbang itu sama dengan nol.
2. Macam-macam gangguan pada ketiga fasor yang tidak seimbang
- Komponen Urutan Positif
Merupakan komponen simetris yang terdiri dari tiga fasor yang sama besarnya, terpisah 120˚, serta memiliki urutan fasa yang sama seperti urutan fasor aslinya. Saat sistem tenaga dalam keadaan normal, terdapat arus dan tegangan urutan positif, sehingga impedansi sistem tenaga pada keadaan normal adalah impedansi urutan positif. Setelah itu ketika terjadi suatu gangguan, cabang yang terganggu pada sistem dapat digantikan dengan perubahan tegangan ∆V = V-V1 dan semua sumber tegangan yang ada pada sistem dihubung singkat, sehingga akan diperoleh arus gangguan ∆I yang mengalir ke dalam sistem, yaitu :
Jika arus awal pada sistem tenaga sebelum terjadi gangguan adalah nol (I = 0), maka arus yang dapat mengalir pada cabang yang mengalami gangguan adalah I1 = -∆I sehingga didapat:
V1 = V – I1Z1
Persamaan diatas merupakan persamaan komponen urutan positif arus dan tegangan pada cabang yang mengalami gangguan.
- Komponen Urutan Negatif
Komponen urutan negatif merupakan komponen yang terdiri dari tiga fasor yang memiliki besar yang sama, terpisah satu dengan yang lainnya dalam fasa sebesar 120˚, dan memiliki urutan fasa yang berlawanan dengan fasor aslinya. Jika pada keadaan normal hanya terdapat komponen urutan positif , maka komponen urutan negatif hanya ada pada saat terjadinya gangguan. Jika tidak ada komponen urutan negatif sebelum terjadinya gangguan, maka apabila terjadi gangguan akan timul perubahan tegangan sebesar –V2, dan arus I2 yang dapat mengalir melalui sistem tenaga ke gangguan, ditunjukkan melalui persamaan berikut ini:
V2 = -I2Z2
Z2 adalah impedansi urutan negatif dan pada umumnya sama dengan impedansi urutan positif.
- Komponen Urutan Nol
Merupakan komponen yang terdiri dari tiga fasor yang memiliki besar yang sama dan tidak ada pergeseran fasa antara fasor yang satu dengan yang lain.
Arus dan tegangan pada komponen urutan nol memiliki fasa yang sama. Sehingga arus urtan nol untuk dapat mengalir pada sistem memerlukan jalan balik/ perputaran (return connection) yang dapat melalui sistem pentanahan netral. Impedansi urutan nol umumnya tidak sama dengan impedansi urutan positif, pada umumnya ini bergantung pada beberapa faktor seperti halnya jenis peralatan pada sistem tenaga, cara menghubungkan lilitan (∆ atau Y), dan cara pentanahan titik netral.
3.Gangguan Berdasarkan Kesimetrisannya
- Gangguan Asimetris, merupakan gangguan yang mengakibatkan tegangan dan arus yang mengalir pada setiap fasanya menjadi tidak seimbang, gangguan ini terdiri dari
- Gangguan Hubung Singkat Satu Fasa ke Tanah
-Gangguan Hubung Singkat Dua Fasa
-Gangguan Hubung Singkat Dua Fasa ke Tanah
- Gangguan Simetris, merupakan gangguan yang terjadi pada semua fasanya sehingga arus maupun tegangan setiap fasanya tetap seimbang setelah gangguan terjadinya. Gangguan ini terdiri dari :
-Gangguan Hubung Singkat Tiga Fasa
-Gangguan Hubung Singkat Tiga Fasa ke Tanah
BAB III
PENUTUP
A.Kesimpulan.
Cara penggunaan rumus-rumus dalam rangkaian R-L-C untuk jenis rangkaian lainnya:
-Dalam rangkaian R-L tidak ada komponen kapasitor (C) maka nilai Xc dan Vc nya = nol (0).
-Dalam rangkaian R-C tidak ada komponen induktor (L) maka nilai XL dan VL nya = nol (0)
-Dalam rangkaian L-C tidak ada komponen resistor (R) maka nilai R dan VR nya = nol (0).
-Dalam rangkaian R-L tidak ada komponen kapasitor (C) maka nilai Xc dan Vc nya = nol (0).
-Dalam rangkaian R-C tidak ada komponen induktor (L) maka nilai XL dan VL nya = nol (0)
-Dalam rangkaian L-C tidak ada komponen resistor (R) maka nilai R dan VR nya = nol (0).
Besarnya arus yang melalui tiap tahanan akan berbeda sesuai dengan nilai tahanannya. Sedangkan beda potensialnya atau tegangan pada tiap masing-masing tahanan adalah sama dengan tegangan sumber.
Untuk tegangannya dapat dianalisis sesuai dengan cara sambungannya. Sambungan secara seri memiliki jumlah seluruh tegangan tiap tahanannya sama dengan tegangan sumber, sedangkan sambungan paralel tegangan setiap tahanannya sama besar.
B.SARAN.
Semoga dari pembahasan dan penjabaran yang telah kami lakukan dapat membantu dalam pemahaman tentang Rangkaian RLC pada mata kuliah Rangkaian listrik.Dari penjelasan Makalah ini banyak akan kekurangan, maka dari itu kami sebagai penyaji mohon maaf.

0 Response to "MAKALAH RANGKAIAN RLC"
Post a Comment